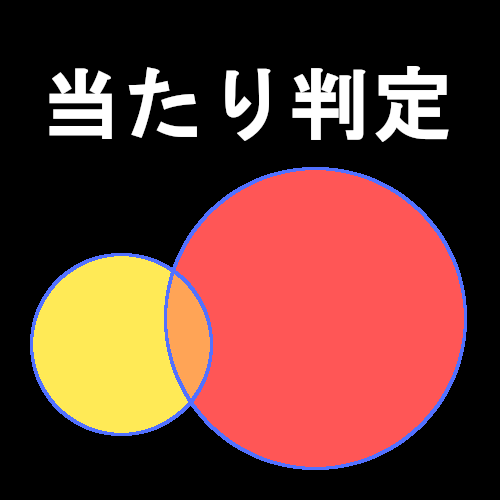
ゲーム画面に表示されるキャラクターや背景はただの画像なので実際に衝突するということはありません。
当たるかどうかはプログラムでチェックしています。
そのプログラムのことを当たり判定と言います。
当たり判定はゲームの面白さを左右する
当たり判定はキャラクターの持つ座標をもとに点や線、円や四角など一定の形で判定されています。
一定の形で判定されるため画像との相性によっては
「うそー!あたってないやん!(´;ω;`)」
みたいな見た目は当たってないけどプログラム上当たるということも起こったりします。
なのでゲームによって使う当たり判定を選んだり、キャラクターに合わせて当たる大きさを修正したりなどしっかり調整しないとゲームの面白さが半減したりします。
アクションゲームやシューティングゲームなどではゲームバランスに影響する特に重要な部分です。
ゲームの当たり判定は数学の知識が必要
数学が苦手な人間には「あ、無理(-_-)」となってしまいそうですが、今回紹介する基本の当たり判定は難しいのでも中学校数学レベルなので頑張ればだれでもできます。
ちなみに記事を書いている筆者は学生時代数学を真面目に勉強しなかったためこの基本の当たり判定すら頭が痛いです。
あなたがもし学生ならちゃんと数学勉強するんだぞ!!
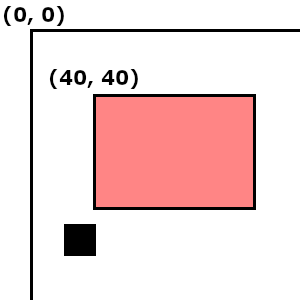
ゲーム画面上の座標について
ゲーム内のキャラクターなどには数学のように座標がついています。
2DゲームならX座標とY座標です。
この2つの座標で画面内の場所を管理しています。
数学の座標と異なるのは原点が画面の左上になりYは下に行くほど大きくなることです。
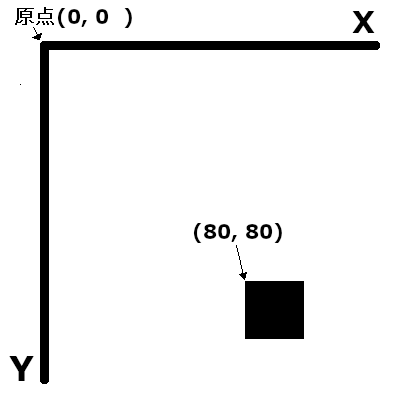
上の図の黒の四角がキャラクターだと思ってください。
こんな感じでキャラクターは画面内の座標を持っています。
キャラクターも左上が原点となっていて座標はこの原点を指しています(ただしキャラクターの原点はゲームエンジンなどによって違う場合があります)。
では次はいよいよ当たり判定です。
単純な位置の判定
最初は当たり判定というほどではないですがプレイヤーの座標がある位置以上または以下というような判定をしてみます。
今回はプレイヤーはただの点だと思ってください。
下図のように赤い場所(x >= 100)のところが当たる場所だった場合
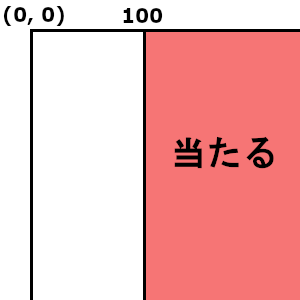
if(player.x >= 100){
//当たったときの処理
}
といった感じになります。
これは簡単ですね。
点と矩形の当たり判定
矩形とは角が直角の四角形のことです。
今回もプレイヤーはただの点です。
下図のようなような赤い範囲(幅100、高さ70)が当たる場所だとした場合
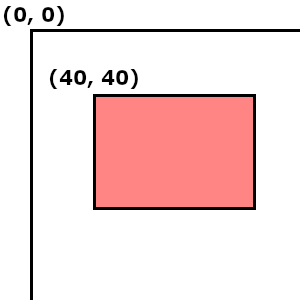
if(player.x >= 40 && player.x <= 140){
if(player.y >= 40 && player.y <= 110){
//当たった処理
}
}
こんな感じの当たり判定になります。
入れ子にして書きましたが「&&」でつなげて一つのif文にしても同じです。
全部の条件を満たせば当たっています。
矩形と矩形の当たり判定
ここからが当たり判定の本番です。
今回はプレイヤーも矩形になります。
下図の黒い四角がプレイヤーです。
プレイヤーは幅20、高さ20あるとします。
説明してきた流れで「どちらかの矩形の4つの頂点のうちの一つでも別の矩形の中に入っていれば当たっている」みたいなこと言ってサクッと説明したいところなんですが実はこの矩形の当たり判定はサクッと説明できるようなものではないんですよね。
まぁそれでもざっくり解説してみます。
まず下図を見てください。
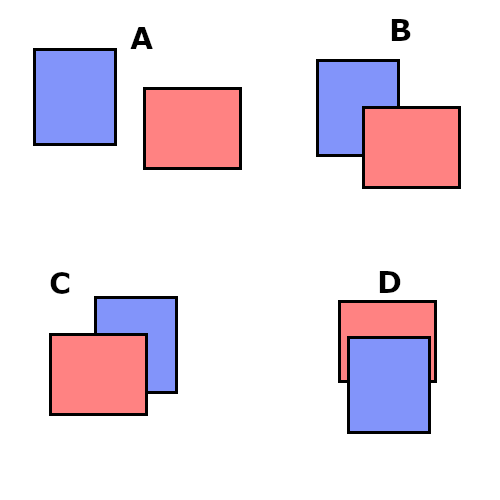
Aは当たっていないですね。
当たるときはB、C、Dみたいな感じなります。
で、当たっていないときは青の矩形の右端(青R)と赤の矩形の左端(赤L)は離れていますつまり青R < 赤Lです。
逆に当たっている所は青R > 赤Lになっています。
しかし赤と青の位置が逆だった場合にこれだけだと当たらないことになります(Aの図の赤と青を入れ替えてみて)。
で入れ替えた場合は赤R > 青Lになったときに当たったことになります。
なのでこの2つを満たすと当たっていることになります。
で、こんどは上と下も同様にやってみてください。
そしてできた2つの式も同時に満たせば確実に当たっていることになります。
if(player.x <= enemy.x + 100 && enemy.x <= player.x + 20){
if(player.y <= enemy.y + 70 && enemy.y <= player.y + 20){
//当たった処理
}
}
ちょっとややこしいですよね。
点と円の当たり判定
次は円の当たり判定です。
とりあえずまたプレイヤーは点で考えてみます。
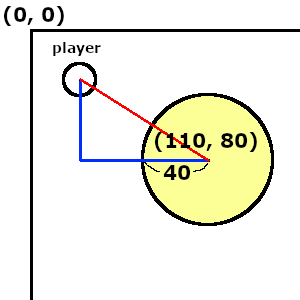
下図のように円があったとします。
円の座標は円の中心で半径は40とします。
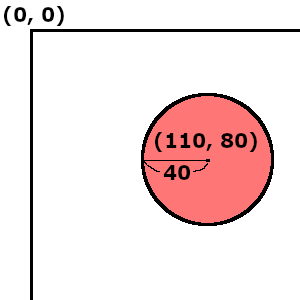
この円の中に入ったら当たったことになります。
この場合、プレイヤーが円の中心座標から半径の距離に入ったら当たりということになりますよね。
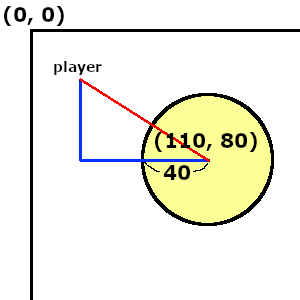
上図のようにプレイヤーの座標と結ぶと三角形ができます。
そして赤い線が円の半径より短くなったら円の中に入っているということになります。
これは三角関数でできますね。
var dx = player.x - enemy.x;
var dy = player.y - enemy.y;
if(dx * dx + dy * dy < 40 * 40){
//当たったときの処理
}
どちらが大きいか分かればいいのできっちりルートまでする必要はないです。
円と円の当たり判定
最後は円と円の当たり判定ですが上のプレイヤーが円になるだけです。
つまりプレイヤーの中心座標と敵キャラの中心座標の距離が「プレイヤーの半径+敵キャラの半径」より小さくなれば当たっていることになります。
プレイヤーの半径を10だとすると
var dx = player.x - enemy.x;
var dy = player.y - enemy.y;
if(dx * dx + dy * dy < (40 + 10) * (40 + 10)){
//当たったときの処理
}
という感じになります。
ちょびっと難しい当たり判定
他にも当たり判定関係の記事があります。
まとめ
とりあえずゲームで使う一番基本の当たり判定はこんな感じです。
これだけできればある程度のゲームを作ることができます。
しかし作るゲームによってはこれだけでは正しく当たり判定ができないことが起こってきます。
ただ、これ以外の方法になってくるとより数学的な知識が必要になって難しくなってきます。
数学の知識がない私はこれ以外の方法を学ぶのにものすごく苦労しています(涙)
もしこれを読んでる君が学生ならしっかり数学の勉強をしてどんどん難しい当たり判定をマスターできるように頑張ってくれ(‘ω’)ノ